Содержание
- Введение
- 1. Поиск в глубину (Depth First Search) и поиск в ширину (Breath First Search)
- 1.1 Проблема заполнения кувшинов
- 1.2 Головоломка "пятнашки"
- 1.3. Базовая логика поиска в ширину и в глубину
- 2. SAT Solvers
- 2.1 Введение
- 2.2 Паззлы Судоку
- 2.3 Паззл Эйнштейна
- 3. Распознавание паттернов (Pattern Recognition)
- 3.1 Введение
- 3.2 Самообучающийся алгоритм на примере игры "камень-ножницы-бумага".
- 3.3 SMT Solvers (задачи выполнимости формул в теориях)
- 4. AlphaZero
- 5. Заключение
Введение
Полный зал, спасибо вам большое! Очень рад видеть всех и приветствую на PyCon. Спасибо, что пригласили меня. Как же долго я ждал возможности прийти на такое долгое живое выступление. Все эти 43 года я этого ждал.
В молодости я смотрел вдохновлявший меня сериал, там был парень по имени Спок с ужасной проблемой. Он был чем-то вроде компьютера с мозгом, а Кирк на глаз оценивал уровень опасности этой проблемы и ее природу.
И вот Спок сказал одну фразу, которая вдохновляет меня всю жизнь: мой компьютер -— это мультитронная модель, сделанная д-ром де Стримом, мозг человека, усиленный реле мгновенного действия, которые можно устанавливать в компьютер. После этой фразы у меня по спине побежали мурашки. Это была не самая лучшая серия, но фраза была важной. Интереснее всего было про усиленный компьютерными реле мозг человека.
Мы используем машины, чтобы стать умнее. Мы долго ждали момента, когда это станет возможно. Алгоритмы известны уже долгое время: поиск в глубину (depth first search), поиск в ширину (breadth first search), поиск по дереву методом Монте-Карло, алгоритмы обхода графа...
Примерно 30 лет назад я читал книги про нейронные сети, ничего нового в этом всем нет. Но вот что изменилось: они совмещаются в интересные сочетания. Алгоритмы стали умнее, вычислительная мощность стала огромной. Эти машины стали умными, поэтому у нас появился новый способ программирования, который не был доступен раньше.
Так вот, темой выступления станет то, что вместо написания программ мы пишем описания проблем, а затем позволяем программам для решения проблем приступить к работе и решить их. Думаю, мы живем в прекрасное время, жить сегодня — очень хорошо. Хочу показать вам некоторые из этих инструментов.
Обычно самый лучший способ демонстрации — это не приложения из реального мира, а игры или пазлы, игрушечные проблемы. Ведь в той части, в которой данные инструменты могут решать данные проблемы, они также способны решать и наши проблемы из реального мира. Поэтому мне бы хотелось, чтобы вы подключили свое воображение, когда я буду показывать вам пазл. Нам нужно будет мысленно переносить его на что-нибудь гораздо более интересное, на оптимизацию наших программ, поиск багов, многопоточный код и т.д.
Не будем затягивать вступление. Я нашел в Интернете фразу, которая сформулирует гораздо лучше, чем все, на что я способен. Выведем ее на экран: "Проще создавать правила, чем искать способ их выполнения". Иногда, если у вас есть описание проблемы, это автоматически дает и решение после передачи этой проблемы программе для ее решения.
Я покажу вам поиск в глубину и поиск в ширину. Звучит не интересно, но на самом деле это мощно. Следующим шагом в развитии возможностей будет то, что называют SAT Solvers (программы для решения задач выполнимости булевых формул). Немного скучно. Потом будут таблицы истинности (truth tables), которые становятся очень большими и очень-очень мощными. Так вот, я покажу вам, на что они способны, и как начать ими пользоваться в Python.
Обучение методом проб и ошибок (reinforcement learning) — очень простая концепция. Мы все время используем ее сами, мы научили машины пользоваться ею. Я покажу простой алгоритм для этого. Потом я отведу вас на такую территорию, на которой многие из вас, возможно, еще не были. Кто из вас слышал про TLA (темпоральная логика действий)? Ну, это фантастика. На самом деле, она становится все популярнее, пока мы говорим. Год назад, наверное, никто в этом зале не знал бы про бы нее. Сколько из вас использует z3? Так, похоже моя работа здесь окончена. Вы, ребята, опережаете свое время. Ладно.
Следующим шагом будет комплексность. Мы объединим все эти инструменты, а также поиск по дереву методом Монте-Карло (Monte Carlo tree search), сверточные нейронные сети (convolutional neural networks) и обучение методом проб и ошибок (reinforcement learning), чтобы победить человеческих существ. Мы поговорим про AlphaZero, который стал прекрасным достижением.
О чем нужно помнить по ходу нашего исследования:
1. Для выражения этих идей нужно очень мало кода.
2. Используются самые обычные инструменты. Насчет всех этих проблем прекрасно то, что лучшими решениями будут не специальные инструменты. То есть, эти инструменты не были специально подогнаны под решение этих проблем.
3. Примеры используются на забавных игрушечных проблемах, поэтому нужно раздвинуть границы воображения, чтобы охватить более сложные проблемы, с которыми можно будет работать при помощи того же инструментария.
Это очень хорошо. Ведь если мы можем довести компьютер так далеко, повышая вычислительную мощность, то мы сможем вывести его за пределы наших собственных возможностей. То есть, достигнем той цели, которую поставил нам Спок. Возможно, та серия была поучительной историей. Мы немного поговорим об этом в конце, чтобы посмотреть, чем все закончится. Возможно, мы все умрем, а возможно — будем собирать урожай пользы от ИИ по мере его развития. Но к этому перейдем в конце.
1. Поиск в глубину (Depth First Search) и поиск в ширину (Breath First Search)
Определенные паззлы можно решать с помощью поиска в глубину или в ширину. Вот эти рисунки, они ведь говорят сами за себя?
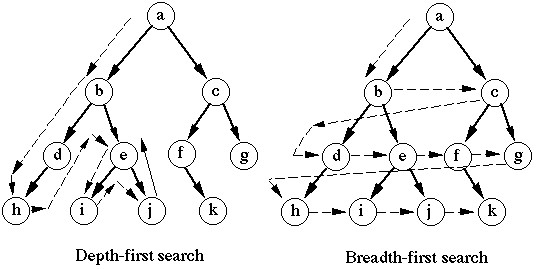
Как работает поиск в глубину: первым делом он идет вниз вертикально или со смещением в сторону. Поэтому он так и называется. Куда движется поиск в ширину? Хорошо.
Итак, разные виды проблем. Иногда, когда мы пытаемся найти самый короткий путь к решению, то пользуемся поиском в ширину. Однако мы увидим, что поиск по дереву методом Монте-Карло, инструменты AlphaZero применяют поиск в глубину.
Они проводят настоящие партии в шахматы, причем по нескольку раз. Потом возвращаются и на основе исхода игры принимают решение о том, какой следует делать ход.
Каким инструментом следует пользоваться в Python, чтобы реализовать поиск в глубину или в ширину? Кто может сказать? Не хочу давать подсказок. Хорошо, collections.deque() — именно тот инструмент, который подходит очень хорошо в данном случае.
Вам решать, следует ли добавлять новые задачи в начало (prepend) очереди (queue), чтобы рабтал поиск в ширину, или в конец (append) очереди, чтобы работал поиск в глубину. На самом деле, код очень простой.
Кстати, все, что я буду показывать на слайдах — код по нотации "О". По мере просмотра слайдов вам встретятся всевозможные примеры, в том числе программа для игры в шахматы. Звучит хорошо, да. Ладно.
Итак, когда-то давно, много лет назад, я написал генеральную программу для решения паззлов, которая работала на широком классе паззлов. В чем базовая идея: программа для решения паззлов ничего не знает про сам паззл. Все что он знает — это как решать паззлы. Нам нужно всего лишь несколько элементов, чтобы описать паззл таким образом, чтобы программа могла найти решение.
Как пользоваться программой. Мы должны понимать стартовую позицию, т.е. тот паззл, который необходимо решить. Далее нам нужно правило (обычно это итератор), чтобы генерировать все возможные ходы из позиции. Также нам нужно уметь распознавать целевое состояние.
Не забываем, что программе ничего не известно о характере игры. Она просто говорит о том, где мы начинаем игру, что мы можем сделать, куда мы пытаемся попасть, а также о том, что она может отвести нас туда. Это фантастика.
Еще можно внести дополнительную информацию:
- через изящный метод __repr__, чтобы отобразать текущую позицию паззла каким-нибудь понятным для нас образом;
- чтобы увидеть, что некоторые позиции сочтены эквивалентными, и их не нужно изучать повторно (например, в крескиках-ноликах все стартовые позиции по углам по сути одинаковые).
Действительно, если начать игру в крестики-нолики в верхнем левом углу, то это изоморф игры, которую начинают в правом нижнем углу. Мы можем научить компьютер узнавать такие позиции и воспринимать их как одинаковые, чтобы ускорить процесс поиска решения.
Эти два момента вовсе не обязательны, чтобы получить решение, но они либо ускоряют поиск либо улучшают оформление процесса.
1.1 Проблема заполнения кувшинов
Классическая простая проблема. Дано: два пустых кувшина емкостью на 3 унции и 5 унций, а также один полный кувшин на 8 унций. Задача: определить последовательность переливов, чтобы в двух самых больших кувшинах было по четыре унции.
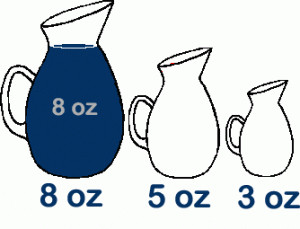
Этот пример нужен нам, чтобы показать вариант работы с программой:
class JugFill(Puzzle):
'''Дано: два пустых кувшина на 3 и 5 л,
полный кувшин на 8 л. Задача: найти такую
последовательность переливов, чтобы в
двух самых больших кувшиха осталось 4 литра.
'''
pos = (0, 0, 8)
capacity = (3, 5, 8)
goal = (0, 4, 4)
def __iter__(self):
for i in range(len(self.pos)):
for j in range(len(self.pos)):
if i==j: continue
qty = min(self.pos[i], self.capacity[j] - self.pos[j])
if not qty: continue
dup = list(self.pos)
dup[i] -= qty
dup[j] += qty
yield JugFill(tuple(dup))
if __name__ == '__main__':
from pprint import pprint
pprint(JugFill().solve())Мы импортируем Puzzle, создаем подкласс и описываем проблему:
- даем подклассу первоначальные позиции в pos: ноль, ноль и восемь унций;
- добавляем ограничения, т.е. емкость кувшинов capacity;
- обозначаем цель goal.
Интересная часть кода — это итератор. Не самый чистый мой код за всю карьеру, но задачу выполняет, а еще он короткий, симпатичный и прост в тестировании. Если мы запустим итератор, по он покажет следующие позиции, возможные варианты разлива после стартовой позиции.
Интересный момент заключается в том, что данная программа для решения ничего не знает про сам паззл. Когда мы ее запускаем, то она начинает его решать и предлагает пример результата. Что же получится во время прогона?
>>> from pprint import pprint
>>> from jug_fill import JugFill
>>> p = JugFill() # Создаем новый паззл
>>> print(p) # Запрашиваем текущую позицию
(0, 0, 8)
>>> p.isgoal() # Мы уже пришли к целевому состоянию?
False
>>> for move in p: # Показать возможные ходы
... print(move)
...
(3, 0, 5)
(0, 5, 3)Мы создаем экземпляр для JugFill(), запрашиваем исходную позицию через print(p) и уточняем, является ли она итоговым целевым состоянием? Затем используем for loop, чтобы получить возможные ходы.
Но если воспользоваться методом solve(), то он начинает подбирать ходы и находит самый короткий путь к решению.
[(0, 0, 8),
(0, 5, 3),
(3, 2, 3),
(0, 2, 6),
(2, 0, 6),
(2, 5, 1),
(3, 4, 1),
(0, 4, 4)]Примерно такие проблемы можно предлагать пятиклассникам, чтобы они заняли свое время и разгадали небольшую тайну. Но если в задаче будет 10-20 кувшинов, то она станет огрмной комплексной проблемой, изоморфом проблемы рюкзака. А ведь она очень сложная, быстро выходит за пределы человеческих возможностей. На самом деле, в какой-то момент она также превзойдет доступные вычислительыне возможности.
Другими словами, изначально проблема была смешная, но если масштабировать ее, то становится гораздо интереснее. Например, с точки зрения оптимизации программы. Все понимают базовую идею о том, как работают программы для решения паззлов: даем описание паззла, она возвращает ответ по шаблону для описания проблемы. После этого программа для решения приступает к работе и находит ответ.
1.2 Головоломка "пятнашки"
Перейдем еще к одному интересному паззлу.

Снова вернусь в свое прошлое, примерно в то время, когда увидел ту серию "Стартрека". Паззл был примерно такой же, с разноцветными элементами, дома у моего деда. Так что я называл его Pa. Чем же он интересен?
Дело было даже не в нем самом. Там надо было просто подвигать блоки туда-сюда и добаться до большого. Он должен был оказаться в нижнем левом углу. Сходу кажется, что все просто. Интерес для меня был в том, что, поскольку мой дед был довольно умным, то никто никогда не мог решить этот паззл. В том чисе все те многочисленные умные люди, которые у него бывали.
Только один человек за всю мою жизнь смог решить его. Это был я. Как у меня получилось? Я написал программу. Одна из самых первых моих программ была написана на бейсике и была посвящена решению этого паззла. Причем еще тогда она делала это примерно так же, как я сделал бы это сейчас.
Когда я увидел решение, то понял, почему было сложно. Комбинации были сильно разветвленные и пересекались между собой. Получался такой очень убористый график с одной дверью на выход. И, если вы не знаете, где дверь, то проходите мимо нее. Но, наконец пройдя в нее, вы увидите еще один график с новой дверью на выход. И этот график вполне мог вернуть вас в самое начало. Вот так вы будете ходить по этому циклу. Количество ходов — огромное.
А решение? Для такого простого на вид паззла, на удивление, оказалось, что до решения 80 ходов.
Для создания представления позиции в данном случае, я сделал красивый вариант с __repr__(), который будет отображать через print() номера блоков. В качестве цели goal я использовал регулярное выражение и указал, что один блок должен в итоге оказаться в обозначенном положении.
from puzzle import Puzzle
import re
class PaPuzzle(Puzzle):
''' PaPuzzle
В этой головломке с пятнашками 9
блоков разных размеров:
один на 2x2, четыре на 1x2, один на 2x1, а
также один на 1x1. Блоки стоят на доске
5x4 с двумя пустыми отсеками на 1x1.
Начиная с обозначенной стартовой
позиции, двигаем блоки, пока 2х2 не
окажется в левом нижнем углу:
1122
1133
45
6788
6799
'''
pos = '11221133450067886799'
goal = re.compile( r'................1...' )
def isgoal(self):
return self.goal.search(self.pos) != None
def __repr__(self):
ans = '\n'
pos = self.pos.replace('0', '.')
for i in [0, 4, 8, 12, 16]:
ans = ans + pos[i:i+4] + '\n'
return ans
xlat = str.maketrans('38975','22264')
def canonical(self):
return self.pos.translate(self.xlat)
block = { (0,-4), (1,-4), (2,-4), (3,-4),
(16,4), (17,4), (18,4), (19,4),
(0,-1), (4,-1), (8,-1), (12,-1), (16,-1),
(3,1), (7,1), (11,1), (15,1), (19,1) }
def __iter__(self):
dsone = self.pos.find('0')
dstwo = self.pos.find('0', dsone+1)
for dest in [dsone, dstwo]:
for adj in [-4, -1, 1, 4]:
if (dest, adj) in self.block: continue
piece = self.pos[dest+adj]
if piece == '0': continue
newmove = self.pos.replace(piece, '0')
for i in range(20):
if 0 <= i+adj < 20 and self.pos[i+adj]==piece:
newmove = newmove[:i] + piece + newmove[i+1:]
if newmove.count('0') != 2: continue
yield PaPuzzle(newmove)
if __name__ == '__main__':
from pprint import pprint
pprint(PaPuzzle().solve())Итак, все как обычно. Программа для решения должна знать стартовую позицию, узнавать целевое положение. Самая интересная часть тоже, как всегда, итератор. Опять-таки, не самый лучший мой код, но ведь ему примерно 15 лет. Было пару апдейтов, но в основном он остался в первозданном виде.
Запустим. У меня тут Python 3.8. Не пользуетесь? Сейчас он на альфе, работать можно. Теперь у нас есть вывод:
[
1122
1133
45..
6788
6799
,
1122
1133
4.5.
6788
6799
,
-- ... ---
7633
7622
1154
1199
..88
,
7633
7622
..54
1199
1188
]Программа дала мне все возможные ходы, со стартовой позиции до конца. Выглядит не очень изящно. Но без __repr__() все было бы на одной строке. Как видим, здесь примерно 88 ходов. Проблема, которую, насколько я знаю, не решил никто из встречавшихся мне умных людей, не заняла много времени.
1.3. Базовая логика поиска в ширину и в глубину
Нужен только один существенный инструмент Python, а именно collections.deque(). Двухсторонний вариант queue.
Во время поиска в ширину мы обрабатываем и удаляем (pop) не изученные позиции из deque. Для каждой позиции мы генерируем следующие возможные ходы и ставим в начало (prepend) очереди deque, содержащей не изученные ходы.
Вам решать, следует ли добавлять новые задачи в начало (prepend) очереди (queue), чтобы рабтал поиск в глубину, или в конец (append) очереди, чтобы работал поиск в ширину. На самом деле, код очень простой.
Мы оставляем для себя возможность повторить последовательность ходов с помощью словаря trail (тропа), который привязывает каждый ход к его предшественнику.
Как вариант оптимизации: пользователь может вызывать метод canonical(), чтобы проверить, будет ли текущая позиция эквивалентна уже изученной.
def solve(pos, depthFirst=False):
queue = deque([pos])
trail = {intern(pos.canonical()): None}
solution = deque()
load = queue.append if depthFirst else queue.appendleft
while not pos.isgoal():
for m in pos:
c = m.canonical()
if c in trail:
continue
trail[intern(c)] = pos
load(m)
pos = queue.pop()
while pos:
solution.appendleft(pos)
pos = trail[pos.canonical()]
return list(solution)Полный код программы для решения
''' Рамочный фреймворк для решения паззлов
Лицензия: MIT
Автор: Raymond Hettinger
Базовые инструкции:
====================
Создаем паззл в виде подкласса для <code>Puzzle()</code>.
Первый этап — выбрать какое-нибудь представление для
отображения состояния программы. Желательно в виде строки (string).
Дать переменной <code>pos</code> стартовую позицию и задать
цель <code>goal</code> для финишной позиции.
Создаем метод <code>__iter__()</code> для расчета всех
возможных новых состояний паззла, которые достижимы через
текущее состояние. Для решения паззла вызвать метод <code>.solve()</code>.
Важное примечание:
Метод <code>__iter__()</code> должен возвращать список или
генератор с экземплярами паззла, а не с их представлениями.
Расширенные инструкции:
1. <code>.solve(depthFirst=1)</code> перезапишет установленный
по умолчанию поиск в ширину. Поиск в глубину следует использовать,
когда известно, что паззл решается за фиксированное количество ходов
(например, задача с 8 ферзями будет решена, когда восьмой появится
на доске; головоломка с треугольником из блоков убирает один
блок на каждом ходу, пока не пропадут все). Поиск в ширину идеально
подходит для случаев, когда нужно найти самое короткое решение
или когда некоторые маршруты могут кружить бесконечно
(например, кубик Рубика можно случайным образом крутить весь день
и никогда не прийти к решению).
2. Подготовить <code>__repr__</code> для структурированного
отображения (pretty printed) текущей позиции. Позиция для паззла
с треугольником лучше всего выглядит с нарисованным полным треугольником.
3. Если целевое состояние нельзя определить в виде строки,
нужно перезаписать метод <code>isgoal()</code>. Например,
паззл с блоками будет решаться в каждом случае, когда блок 1
находится в нижнем левом углу. Неважно, где остальнеы блоки.
Поэтому <code>isgoal()</code> будет определен таким образом,
чтобы проверять нижний левый угол и возвращать булево выражение.
4. Некоторые паззлы можно упростить, если обозначать симметричные
позиции как одинаковые. Перезаписываем метод <code>.canonical()</code>,
чтобы выбрать одно из эквивалентных положений как репрезентативное.
Это позволит программе для решения распознавать маршруты,
аналогичные ранее изученным. В крестиках-ноликах верхний левый угол
на первом ходу симметрически эквивалентен ходу с верхнего правого угла.
Поэтому существует все три первых хода (угол, центр, по бокам от центра).
'''
from collections import deque
from sys import intern
import re
class Puzzle:
pos = "" # стартовая позиция по умолчанию
goal = "" # финишная позиция, которую использует isgoal()
def __init__(self, pos=None):
if pos: self.pos = pos
def __repr__(self): # возвращает представление в виде строки, чтобы отобразить объект
return repr(self.pos)
def canonical(self): # возвращает представление в виде строки после поправки на симметрию
return repr(self)
def isgoal(self):
return self.pos == self.goal
def __iter__(self): # возвращает список объектов по данному классу
if 0: yield self
def solve(pos, depthFirst=False):
queue = deque([pos])
trail = {intern(pos.canonical()): None}
solution = deque()
load = queue.append if depthFirst else queue.appendleft
while not pos.isgoal():
for m in pos:
c = m.canonical()
if c in trail:
continue
trail[intern(c)] = pos
load(m)
pos = queue.pop()
while pos:
solution.appendleft(pos)
pos = trail[pos.canonical()]
return list(solution)К чему я это все. Мы готовим описание проблемы, программа ее решает. Поиск в глубину и в ширину — замечательные и мощные. Стал ли мир интереснее, когда появились такие инструменты. Да, конечно.
2. SAT Solvers
2.1 Введение
Давайте немного поговорим на технические темы на нашей технической конференции. Сейчас я покажу немного математики, которая напомнит вам худшие дни в колледже, и вы все встанете и уйдете.
Итак, SAT Solvers (программы для решения задач выполнимости булевых формул). Суть в том, что они решают проблемы, которые описываются с помощью формул логики высказываний (propositional logic). На этом месте многие разворачиваются и убегают.
Идея логики высказываний в том, что если взять какое-нибудь высказывание о проблеме, например: "Если шина спустила, то ее надо снять и отвезти на заправку", то наша задача в том, чтобы сначала перевести его в логические выражения. Возьмем каждую часть высказывания и присвоим ей переменные.
P — шина спустила.
Q — нужно снять шину.
R — нужно отвезти шину на заправку.
Затем записываем выражение в символьной форме, это не трудно:
P → (Q ^ R)
Возможно, вы уже забыли, как все это делать. Но, если есть желание пользоваться этими инструментами, знания придется возродить. Пользуйтесь этими слайдами как пошаговой инструкцией, чтобы вновь приобрести нужные знания.
Итак, перед нами таблица истинности, которая показывает, когда выражение будет истинным (T — истинное, F — ложное). В первых трех столбцах будут состояния, а в последнем будет состояние на выходе. В нем задается сам вопрос.
| P | Q | R | P → (Q ∧ R) |
|---|---|---|---|
| T | T | T | T |
| T | T | F | F |
| T | F | T | F |
| T | F | F | F |
| F | T | T | T |
| F | T | F | T |
| F | F | T | T |
| F | F | F | T |
Не все, но многие SAT Solvers могут дать пример ряда, где T будет означать True. Это все звучит не особо интересно, потому что мы можем просто пройтись циклом и найти T, а затем вывести его через print(). Это все звучит мощно? Нет, не звучит. Это не особо интересная проблема.
Интересными такие таблицы становятся с размером. У нас три переменные, и мы получили два в третьей степени, т.е. восемь рядов. Получается, если у нас будет десять переменных, то в результате будет два в десятой степени. Миллион рядов. А если 20 переменных? Потрясающе, мы будем расти дальше. На 30 переменных мы перейдем к миллиардам.
А если будет тысяча переменных? Проблема становится сложной. Состояний окажется больше, чем атомов во вселенной. Выглядит ли это все поддающимся вычислительной обработке? Не выглядит. Можно даже доказать, что данную проблему обработать нельзя. Однако большинство проблем реального мира содержат в себе симметрии и паттерны.
Мы живем в прекрасное время. Пока я живу, каждый год кто-нибудь хватается за эту проблему и говорит о том, что в ней есть внутренние паттерны, которыми можно пользоваться и которые можно эксплуатировать в реальной жизни. Каждый год SAT solvers становятся умнее. Не понемножку умнее, а намного умнее. Сегодня уже не следует удивляться тому, что мы прогоняем SAT-проблемы с миллионом переменных и пользуемся этими инструментами, чтобы находить решения.
Азимов говорил, что, если технология будет в достаточной степени продвинутой, то ее нельзя будет отличить от магии. Именно с помощью магии мы находим ответы на данные проблемы. Поэтому это все для нас важно. Ведь мы можем решать эти проблемы с тысячами и даже миллионами переменных.
Как это сделать в Python? Есть такой инструмент под названием pycosat. Это не единственный вариант для решения проблем, есть и другие. Но, чтобы пользоваться данными инструментами, нужно производить впечатление математика! Например, нужно быть способным произносить фразу "конъюнктивная нормальная форма" (conjunctive normal form) как нечто банальное. Попробуйте, получится без улыбки? Что она означает? Это произведение сумм.
Вернемся к нашей проблеме и перепишем выражение в виде конъюнктивной нормальной формы.
(¬P ∨ Q) ∧ (¬P ∨ R)Во время работы с SAT solvers часто приходится писать отрицательные переменные. В pycosat переменную P надо писать как 1, потому что она стоит первой. Поэтому −P надо писать как −1, минусом обозначая отрицательность.
Мы передаем список кортежей, при этом каждый разрыв обозначается отдельным кортежем:
>>> pprint(list(pycosat.itersolve([(-1, 2), (-1, 3)])), width=20)
[[-1, 2, 3],
[-1, 2, -3],
[-1, -2, 3],
[-1, -2, -3],
[1, 2, 3]]Как видите, второй переменной является 2, поэтому она обозначается через −1 и 3. На выходе у нас оказалось 5 рабочих состояний.
Какая здесь будет главная проблема? Все эти инструменты не выглядят по-человечески, а возможность сделать их более понятными в них не предусмотрена. Поэтому инструмент для этого я написал сам и дарю его вам. Кода там немного. По сути, он принимает понятные для нас фразы и переводит их.
Начнем с наших выражений, чтобы в них были символы вместо цифр и ~ для отрицательности вместо минуса:
>>> translate([['~P', 'Q'],['~P', 'R']])[0]
[(-1, 2), (-1, 3)]Как видим, мой инструмент для перевода превратил вводные данные с P, Q и R в числа. Наверное, для вас это уже выглядит получше.
На самом деле, иногда трудно перевести задачу в конъюнктивную нормальную форму. Обычно мы начинаем с чего-то вот такого, дизъюнктивной нормальной формы (disjunctive normal form):
¬P ∨ (Q ∧ R)Переводить из нее в конъюнктивную — настоящая боль. Было бы неплохо, чтобы компьютер делал это для нас. Поэтому я написал from_dnf для конвертации:
>>> from_dnf([['~P'], ['Q', 'R']])
[('~P', 'Q'), ('~P', 'R')]По сути, код принимает от вас что-то для вас понятное и преобразует в нечто другое, зато понятное для машины, для pycosat, с помощью функции solve_all:
>>> cnf = from_dnf([['~P'], ['Q', 'R']])
>>> solve_all(cnf, True)
[['~P', 'Q', 'R'],
['~P', 'Q', '~R'],
['~P', '~Q', 'R'],
['~P', '~Q', '~R'],
['P', 'Q', 'R']]Возможно, нам не стоит пользоваться такими именами переменных как P, Q и R. Давайте попробуем на проблеме со спущенной шиной и поездкой на заправку. У нас будут все эти истинные выражения, и все будет выглядеть немного получше:
>>> cnf = from_dnf([['~FlatTire'], ['NeedToRemove', 'GotoGasStation']])
>>> solve_all(cnf, True)
[['~FlatTire', 'NeedToRemove', 'GotoGasStation'],
['~FlatTire', 'NeedToRemove', '~GotoGasStation'],
['~FlatTire', '~NeedToRemove', 'GotoGasStation'],
['~FlatTire', '~NeedToRemove', '~GotoGasStation'],
['FlatTire', 'NeedToRemove', 'GotoGasStation']]Итак, мы обсудили все эти инструменты. Дарю их вам. Надеюсь, будете пользоваться. Также я написал несколько функций более высокого порядка для удобства. Ведь про дизъюнктивную форму легко говорить, но ее скучно писать.
Поэтому у меня есть несколько функций, которые строят конъюнктивную форму напрямую из ограничений, обозначенных квантификаторами.
# Выражение для обозначения того, что как минимум одна переменная среди A, B и C является истинной
>>> some_of(['A', 'B', 'C'])
[['A', 'B', 'C']]
# Выражение для обозначения того, что только одна переменная среди A, B и C является истинной
>>> one_of(['A', 'B', 'C'])
[('A', 'B', 'C'),
('~A', '~B'),
('~A', '~C'),
('~B', '~C')]
# Выражение для обозначения того, что не более одной переменной среди A, B и C является истинной
>>> Q(['A', 'B', 'C']) <= 1
[('~A', '~B'),
('~A', '~C'),
('~B', '~C')]На выходе получается довольно изящная форма для ввода данных, потому что огромное количество проблем помещается в этот формат.
2.2 Паззлы Судоку
Полагаю, в какой-то момент многие начинают интересоваться машинным обучением и программами для решения проблем. На каком-то этапе вы даже напишете программу для Судоку.
На самом деле, ничего сложного. Проведем опрос. Кто здесь писал такую программу? Многие. Я тоже, очень давно. Сейчас я не про то, что буду отказываться от своей старой программы для решения Судоку. Независимо от объема затраченных усилий я не смогу сделать ее лучше того, что у нас есть. А есть у нас общая программа для решения головоломок.
Из года в год ее полировали на конференциях разные люди, которые вызывались добровольцами и вносили мелкие улучшения в базовую программу.
Поэтому, если вам хочется получить хорошее решение, например, для очень сложного Судоку сто на сто (с которым не справится большинство программ), то мне нужно всего лишь подготовить описание проблемы, передать его действительно крутой программе для решения паззлов и предоставить остальное ей.
Итак, интересной для нас частью является не написание программы для решения Судоку, а подготовка описания проблемы. Решать ее для нас будет программа.
Как будет выглядет паззл:
8 6|4 3|
5 | | 7
| 2 |
---+---+---
32 | 8 | 5
8| 5 |4
1 | 7 | 93
---+---+---
| 4 |
9 | | 4
|6 7|2 8Мы введем его в виде строки (string) вот в таком представлении:
s = ('8 64 3 5 7 2 '
'32 8 5 8 5 4 1 7 93'
' 4 9 4 6 72 8')Мы ожидаем, что компьютер выдаст следующий ответ:
876|413|529
452|968|371
931|725|684
---+---+---
329|184|756
768|359|412
145|276|893
---+---+---
283|541|967
697|832|145
514|697|238У меня, вроде, было пять таких паззлов. У нас будет паззл для ввода и решение. Предлагаю вам весь исходный код:
from sat_utils import solve_one, one_of, basic_fact
from sys import intern
from pprint import pprint
n = 3
grid = '''\
AA AB AC BA BB BC CA CB CC
AD AE AF BD BE BF CD CE CF
AG AH AI BG BH BI CG CH CI
DA DB DC EA EB EC FA FB FC
DD DE DF ED EE EF FD FE FF
DG DH DI EG EH EI FG FH FI
GA GB GC HA HB HC IA IB IC
GD GE GF HD HE HF ID IE IF
GG GH GI HG HH HI IG IH II
'''
values = list('123456789')
table = [row.split() for row in grid.splitlines()]
points = grid.split()
subsquares = dict()
for point in points:
subsquares.setdefault(point[0], []).append(point)
# Groups: rows + columns + subsquares
groups = table[:] + list(zip(*table)) + list(subsquares.values())
del grid, subsquares, table # analysis requires only: points, values, groups
def comb(point, value):
'Format a fact (a value assigned to a given point)'
return intern(f'{point} {value}')
def str_to_facts(s):
'Convert str in row major form to a list of facts'
return [comb(point, value) for point, value in zip(points, s) if value != ' ']
def facts_to_str(facts):
'Convert a list of facts to a string in row major order with blanks for unknowns'
point_to_value = dict(map(str.split, facts))
return ''.join(point_to_value.get(point, ' ') for point in points)
def show(flatline):
'Display grid from a string (values in row major order with blanks for unknowns)'
fmt = '|'.join(['%s' * n] * n)
sep = '+'.join(['-' * n] * n)
for i in range(n):
for j in range(n):
offset = (i * n + j) * n**2
print(fmt % tuple(flatline[offset:offset+n**2]))
if i != n - 1:
print(sep)
for given in [
'53 7 6 195 98 6 8 6 34 8 3 17 2 6 6 28 419 5 8 79',
' 75 4 5 8 17 6 36 2 7 1 5 1 1 5 8 96 1 82 3 4 9 48 ',
' 9 7 4 1 6 2 8 1 43 6 59 1 3 97 8 52 7 6 8 4 7 5 8 2 ',
'67 38 921 85 736 1 8 4 7 5 1 8 4 2 6 8 5 175 24 321 61 84',
'27 15 8 3 7 4 7 5 1 7 9 2 6 2 5 8 6 5 4 8 59 41',
'8 64 3 5 7 2 32 8 5 8 5 4 1 7 93 4 9 4 6 72 8',
]:
cnf = []
# each point assigned exactly one value
for point in points:
cnf += one_of(comb(point, value) for value in values)
# each value gets assigned to exactly one point in each group
for group in groups:
for value in values:
cnf += one_of(comb(point, value) for point in group)
# add facts for known values in a specific puzzle
for known in str_to_facts(given):
cnf += basic_fact(known)
# solve it and display the results
result = facts_to_str(solve_one(cnf))
show(given)
print()
show(result)
print('=-' * 20)Здесь я не занимался логикой, не делал ничего из того, что остальные обычно делают во время работы над программой для Судоку. Я просто дал описание проблемы, т.е. внешнего вида поля и того как его заполнять. В основном это выглядит как преобразование вводных данных и вывод результата.
Логическая часть программы, по сути, представляет собой код для каждой точки (point). Каждая точка принимает одно значение, т.е. можно ввести в ячейку одну цифру. Получается своего рода инъекция байтов, взаимоотношения один на один, которые описывают паззл в общем смысле.
Программа для решения паззлов ничем не ограничена. В нашем случае будет ограничение в рамках конкретного паззла. У нас есть несколько заключений, которые нам известны по поводу данного паззла, т.е. какие цифры куда пойдут.
В этом коде всего пять строк уходит на полное описание Судоку. Еще две строки нужно для описания конкретного Судоку. В результате получается немного проще, если сравнивать с вашими Судоку. Не забывайте, данная программа масштабируется на действительно сложные проблемы.
2.3 Паззл Эйнштейна
Что дальше? Паззл, созданный Эйнштейном. Да, никто из вас не повелся. Говорят, что его создал Эйнштейн, но это неправда. Он просто сказал, что решить его может менее 2 % населения. Это миф. Оба данных факта неверны.
Паззл действительно знаменитый. Посмотрим на описание:
- Есть пять домов уникальных цветов: синий, зеленый, красный, белый и желтый.
- В каждом живет человек уникальной национальности: британец, датчанин, немец, норвежец и швед.
- Каждый человек пьет уникальный напиток: пиво, кофе, молоко, чай и воду.
- Каждый человек курит сигары уникальной марки: Blue Master, Dunhill, Pall Mall, Prince и смесь.
- У каждого человека есть уникальное животное: коты, птицы, собаки, рыбки и лошади.
Обратите внимание на слово "уникальный". Оно означает, что мы будем использовать одну из ранее упомянутых функций. Это будет двоичный поиск (bisection) как раньше. Каждое из этих значений уникальным образом присваивается одному дому.
Это было описание ничем не ограниченной проблемы. Теперь перейдем к ограничениям:
- Британец живет в красном доме.
- Швед держит собак.
- Датчанин пьет чай.
- Зеленый дом слева от белого, рядом с ним.
- Владелец зеленого дома пьет кофе.
- Курильщик Pall Mall разводит птиц.
- Владелец желтого дома курит Dunhill.
- Жилец стоящего по центру дома пьет молоко.
- Норвежец живет в первом доме.
- Курильщик смеси живет рядом с тем, кто держит котов.
- Владелец лошадей живет рядом с курильщиком Dunhill.
- Курильщик Blue Master пьет пиво.
- Немец курит Prince.
- Норвежец живет рядом с синим домом.
- Курильщик смеси живет рядом с человеком, пьющим воду.
Вопрос: кто разводит рыбок?
Интересно расписано. Может, вам интересно решить данную проблему вручную, а ведь именно в этом я совершенно не заинтересован на данный момент. Я хочу как раз получить ответ, который выскочит автоматически.
Это будет больше, чем просто ответ на данный конкретный вопрос. Будет в точности показано, какое значение присвоено каждому дому.
Интересный момент в том, каким образом мы составим описание паззла. Мы обозначим номера домов, группы и соответствия между строками:
['1 norwegian', '1 yellow', '1 cat', '1 water', '1 dunhill',
'2 dane', '2 blue', '2 horse', '2 tea', '2 blends',
'3 brit', '3 red', '3 bird', '3 milk', '3 pall mall',
'4 german', '4 green', '4 fish', '4 coffee', '4 prince',
'5 swede', '5 white', '5 dog', '5 root beer', '5 blue master']То есть, при описании проблемы наша задача — перевести задачу в код, в том чисе заданные ограничения, например то, что британец живет в красном доме. Затем просто запускаем программу на поиск ответа. И все.
Код для решения паззла Эйнштейна:
from sat_utils import solve_one, from_dnf, one_of
from sys import intern
from pprint import pprint
houses = ['1', '2', '3', '4', '5' ]
groups = [
['dane', 'brit', 'swede', 'norwegian', 'german' ],
['yellow', 'red', 'white', 'green', 'blue' ],
['horse', 'cat', 'bird', 'fish', 'dog' ],
['water', 'tea', 'milk', 'coffee', 'root beer'],
['pall mall', 'prince', 'blue master', 'dunhill', 'blends' ],
]
values = [value for group in groups for value in group]
def comb(value, house):
'Format how a value is shown at a given house'
return intern(f'{value} {house}')
def found_at(value, house):
'Value known to be at a specific house'
return [(comb(value, house),)]
def same_house(value1, value2):
'The two values occur in the same house: brit1 & red1 | brit2 & red2 ...'
return from_dnf([(comb(value1, i), comb(value2, i)) for i in houses])
def consecutive(value1, value2):
'The values are in consecutive houses: green1 & white2 | green2 & white3 ...'
return from_dnf([(comb(value1, i), comb(value2, j))
for i, j in zip(houses, houses[1:])])
def beside(value1, value2):
'The values occur side-by-side: blends1 & cat2 | blends2 & cat1 ...'
return from_dnf([(comb(value1, i), comb(value2, j))
for i, j in zip(houses, houses[1:])] +
[(comb(value2, i), comb(value1, j))
for i, j in zip(houses, houses[1:])]
)
cnf = []
# each house gets exactly one value from each attribute group
for house in houses:
for group in groups:
cnf += one_of(comb(value, house) for value in group)
# each value gets assigned to exactly one house
for value in values:
cnf += one_of(comb(value, house) for house in houses)
cnf += same_house('brit', 'red')
cnf += same_house('swede', 'dog')
cnf += same_house('dane', 'tea')
cnf += consecutive('green', 'white')
cnf += same_house('green', 'coffee')
cnf += same_house('pall mall', 'bird')
cnf += same_house('yellow', 'dunhill')
cnf += found_at('milk', 3)
cnf += found_at('norwegian', 1)
cnf += beside('blends', 'cat')
cnf += beside('horse', 'dunhill')
cnf += same_house('blue master', 'root beer')
cnf += same_house('german', 'prince')
cnf += beside('norwegian', 'blue')
cnf += beside('blends', 'water')
pprint(solve_one(cnf))Еще мне пришлось написать пару вспомогательных функций, взяв их из другой программы, о которой мы уже поговорили. Еще дал функциям более человеческие названия. Всегда делайте это. Несложно сделать, но облегчает жизнь очень сильно.
Это поможет вам писать генеральные программы для решения проблем. Им можно пользоваться уже через несколько минут, а в противном случае у вас уйдет два дня только на код для проблемы.
'Рабочие функции, чтобы взаимодействие с pycosat проходило на более человечном языке'
__author__ = 'Raymond Hettinger'
import pycosat # https://pypi.python.org/pypi/pycosat
from itertools import combinations
from functools import lru_cache
from sys import intern
def make_translate(cnf):
"""Make translator from symbolic CNF to PycoSat's numbered clauses.
Return a literal to number dictionary and reverse lookup dict
>>> make_translate([['~a', 'b', '~c'], ['a', '~c']])
({'a': 1, 'c': 3, 'b': 2, '~a': -1, '~b': -2, '~c': -3},
{1: 'a', 2: 'b', 3: 'c', -1: '~a', -3: '~c', -2: '~b'})
"""
lit2num = {}
for clause in cnf:
for literal in clause:
if literal not in lit2num:
var = literal[1:] if literal[0] == '~' else literal
num = len(lit2num) // 2 + 1
lit2num[intern(var)] = num
lit2num[intern('~' + var)] = -num
num2var = {num:lit for lit, num in lit2num.items()}
return lit2num, num2var
def translate(cnf, uniquify=False):
'Translate a symbolic cnf to a numbered cnf and return a reverse mapping'
# DIMACS CNF file format:
# http://people.sc.fsu.edu/~jburkardt/data/cnf/cnf.html
if uniquify:
cnf = list(dict.fromkeys(cnf))
lit2num, num2var = make_translate(cnf)
numbered_cnf = [tuple([lit2num[lit] for lit in clause]) for clause in cnf]
return numbered_cnf, num2var
def itersolve(symbolic_cnf, include_neg=False):
numbered_cnf, num2var = translate(symbolic_cnf)
for solution in pycosat.itersolve(numbered_cnf):
yield [num2var[n] for n in solution if include_neg or n > 0]
def solve_all(symcnf, include_neg=False):
return list(itersolve(symcnf, include_neg))
def solve_one(symcnf, include_neg=False):
return next(itersolve(symcnf, include_neg))
############### Support for Building CNFs ##########################
@lru_cache(maxsize=None)
def neg(element) -> 'element':
'Negate a single element'
return intern(element[1:] if element.startswith('~') else '~' + element)
def from_dnf(groups) -> 'cnf':
'Convert from or-of-ands to and-of-ors'
cnf = {frozenset()}
for group in groups:
nl = {frozenset([literal]) : neg(literal) for literal in group}
# The "clause | literal" prevents dup lits: {x, x, y} -> {x, y}
# The nl check skips over identities: {x, ~x, y} -> True
cnf = {clause | literal for literal in nl for clause in cnf
if nl[literal] not in clause}
# The sc check removes clauses with superfluous terms:
# {{x}, {x, z}, {y, z}} -> {{x}, {y, z}}
# Should this be left until the end?
sc = min(cnf, key=len) # XXX not deterministic
cnf -= {clause for clause in cnf if clause > sc}
return list(map(tuple, cnf))
class Q:
'Quantifier for the number of elements that are true'
def __init__(self, elements):
self.elements = tuple(elements)
def __lt__(self, n: int) -> 'cnf':
return list(combinations(map(neg, self.elements), n))
def __le__(self, n: int) -> 'cnf':
return self < n + 1
def __gt__(self, n: int) -> 'cnf':
return list(combinations(self.elements, len(self.elements)-n))
def __ge__(self, n: int) -> 'cnf':
return self > n - 1
def __eq__(self, n: int) -> 'cnf':
return (self <= n) + (self >= n)
def __ne__(self, n) -> 'cnf':
raise NotImplementedError
def __repr__(self) -> str:
return f'{self.__class__.__name__}(elements={self.elements!r})'
def all_of(elements) -> 'cnf':
'Forces inclusion of matching rows on a truth table'
return Q(elements) == len(elements)
def some_of(elements) -> 'cnf':
'At least one of the elements must be true'
return Q(elements) >= 1
def one_of(elements) -> 'cnf':
'Exactly one of the elements is true'
return Q(elements) == 1
def basic_fact(element) -> 'cnf':
'Assert that this one element always matches'
return Q([element]) == 1
def none_of(elements) -> 'cnf':
'Forces exclusion of matching rows on a truth table'
return Q(elements) == 0На этом все по SAT Solvers. Хочу лишь сказать, что это все очень круто. Я показал вам игрушечные проблемы, но они масштабируются до огромных. Представьте себе данную проблему с миллионом переменных. Где могут такие встречаться? Например в Anaconda. Это их сфера.
Но Conda приходится принимать решения при наличии конфликта между пакетами, а также сталкиваться с проблемами зависимостей. Эта проблема будет сложной, когда пакетов очень много.
В Conda используется pycosat, используется именно эта методика. Причем для решения довольно сложных проблем реального мира.
3. Распознавание паттернов (Pattern Recognition)
3.1 Введение
Давайте быстро обозначим проблему. Мне нужно, чтобы мой сын ел брокколи. Ему — семь. На самом деле, он, конечно, ест брокколи, и для меня это поразительно, потому что я сам дошел до этого гораздо позже. Так что этой проблемы в реальности уже нет.
Какие стратегии я обсуждал с Рейчел? Мы могли давать брокколи один раз в неделю, пока он не привыкнет. Еще я мог предложить ему посмотреть любимый фильм, когда он закончит с брокколи. Все родители пробовали что-то такое, подобные хитрости. Можно еще предлагать конфеты или приводить в пример лучшего друга, который ест брокколи. Или вообще заявить, что вы не встанете из-за стола, молодой человек, пока не доедите брокколи. Можно давить на логику и объяснять, что брокколи очень полезная, она — прекрасный источник витаминов.
Все это — разные стратегии. Появляется вопрос: какую применять. Можно пробовать случайным образом и смотреть, работает или нет. Работающие стратегии будут выбираться почаще, а по мере снижения эффективности — пореже. Это и есть обучение методом проб и ошибок (reinforcement learning).
О, вы снимаете мой экран? Значит у меня хорошие слайды, и я хорошо поработал. На самом деле, я отдам все слайды, и даже не в виде картинок. Они будут в HTML. Так что вы сможете прогонять код сразу. Но можно потом сделать фото, конечно.
3.2 Самообучающийся алгоритм на примере игры "камень-ножницы-бумага"
Ладно. Вместо поедания брокколи давайте перейдем к игре "камень-ножницы-бумага". Мы выбираем стратегию случайным образом и смотрим, работает или нет. В связи с этим есть такой интересный момент. Впервые такая программа мне встретилась в компьютерном журнале больше 30 лет назад. Она меня поразила, потому что данная игра не предусматривает победу. Прогресс обнуляется.
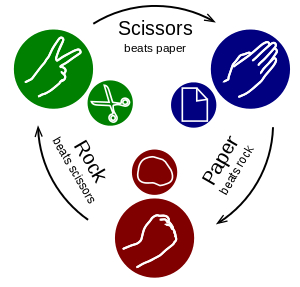
Но представим, что вы в состоянии предугадывать действия оппонента. Благодаря этому ваш результат будет лучше среднего. Вам нужно найти паттерн и определить порядок действий оппонента. Поэтому данная игра становится интереснее, если мы предусматриваем переигровку.
Логику набора баллов очень легко представить в виде словаря:
# scorer['RS'] -> 1 означает Rock затупит Scissors, т.е. +1 для первого игрока.
scorer = dict(SP=1, PR=1, RS=1, PS=-1, RP=-1, SR=-1, SS=0, PP=0, RR=0)Подумаем, как можно выигрывать (не проигрывать):
- Если играть по случайной схеме, мы точно будем проигрывать не больше чем в 1/3 случаев;
- Если оппонент полностью предсказуем, то мы сможем всегда выигрывать;
- В реальном мире людям трудно симулировать абсолютно случайный порядок или наличие плана для победы:
-- небольшое предпочтение paper;
-- частый выбор rock после scissors;
-- если мы выбираем paper, то на следующем раунде оппонент часто выбирает scissors;
-- оппонент часто повторяет наш выбор из предыдущего раунда;
- Другими словами, могут присутствовать паттерны, которые мы можем определить и использовать, чтобы выигрывать чаще, чем в 1/3 случаев.
Какой мы используем подход:
- Генерируем несколько конкурирующих стратегий для распознавания паттернов;
- Среди подходов к обучению методом проб и ошибок выбираем стратегии методом многорукого бандита (multi-arm bandit);
- Базовая логика:
for trial in range(trials):
# выбираем вариант
# получаем вариант оппонента
# определяем победителя
# обновляем историю ходов и удельный вес стратегийЯ обозначу несколько навыков работы с Python для понимания кода. Сейчас нет времени их рассмаривать, но вы будете немного лучше понимать Python. Возможно, вы не умели переставлять местами ключи (keys) и значения (values), группировать пары, пользоваться новой функцией случайного выбора и др.
- itertools.chain() объединяет несколько итерируемых объектов (iterables) в один:
>>> from itertools import chain
>>> list(chain('RPRPS', 'RPS'))
['R', 'P', 'R', 'P', 'S', 'R', 'P', 'S']- itertools.cycle() повторяет одну и ту же последовательность снова и снова:
>>> from itertools import cycle, islice
>>> list(islice(cycle('RPS'), 9))
['R', 'P', 'S', 'R', 'P', 'S', 'R', 'P', 'S']- collections.Counter() считает периодичность вводимых данных:
>>> from collections import Counter
>>> Counter('RPRPSRPSR')
Counter({'R': 4, 'P': 3, 'S': 2})- Counter.most_common(n) выбирает самые частые повторения n:
>>> Counter('RPRPSRPSR').most_common(2)
[('R', 4), ('P', 3)]- zip(*somedict.items()) расставляет элементы по отдельным ключам и значениям:
>>> d = dict(R=4, P=3, S=2)
>>> keys, values = zip(*d.items())
>>> keys
('R', 'P', 'S')
>>> values
(4, 3, 2)- zip(a, a[1:]) группирует вводимые данные в пересекающиеся диаграфы:
>>> a = 'abcde'
>>> list(zip(a, a[1:]))
[('a', 'b'), ('b', 'c'), ('c', 'd'), ('d', 'e')]- random.choices(population, weights)[0] делает выбор из популяции на основе удельного веса:
>>> from random import choices
>>> choices(['R', 'P', 'S'], [6, 3, 1], k=10)
['P', 'P', 'R', 'S', 'R', 'P', 'P', 'R', 'R', 'P']
>>> Counter(_)
Counter({'P': 5, 'R': 4, 'S': 1})Мы определяем игру "камень-ножницы-бумага" в коде:
''' Базовый алгоритм обучения для состязательных
игр с нулевой суммой между двумя игроками и совершенной информацией.
Генеральный подход: Создать список стратегий на основе
распознавания паттернов. Использовать стратегию многорукого бандита
для определения выигрышных стратегий.
'''
from collections import Counter
from random import choices, choice
from itertools import chain, cycle
from pprint import pprint
# Правила игры ################################
# https://en.wikipedia.org/wiki/Rock%E2%80%93paper%E2%80%93scissors
# scorer['RS'] -> 1 означает, что Rock затупит Scissors, т.е. +1 первому игроку.
scorer = dict(SP=1, PR=1, RS=1, PS=-1, RP=-1, SR=-1, SS=0, PP=0, RR=0)
# Scissors режет Paper; Paper оборачивает Rock; Rock затупит Scissors
ideal_response = {'P': 'S', 'R': 'P', 'S': 'R'}
options = ['R', 'P', 'S']
# Инструменты для стратегии #############################
def select_proportional(events, baseline=()):
rel_freq = Counter(chain(baseline, events))
population, weights = zip(*rel_freq.items())
return choices(population, weights)[0]
def select_maximum(events, baseline=()):
rel_freq = Counter(chain(baseline, events))
return rel_freq.most_common(1)[0][0]
# Стратегии #####################################
def random_reply(p1hist, p2hist):
return choice(options)
def single_event_proportional(p1hist, p2hist):
""" Если оппонент играет R в 2/3 случаев,
выбираем P в 2/3 случаев.'
"""
prediction = select_proportional(p2hist, options)
return ideal_response[prediction]
def single_event_greedy(p1hist, p2hist):
""" Если оппонент играет R чаще, чем P или S,
всегда выбираем выбираем P.'
"""
prediction = select_maximum(p2hist, options)
return ideal_response[prediction]
def digraph_event_proportional(p1hist, p2hist):
""" Если в прошлом раунде оппонент выбрал S,
но играет R в 2/3 случаев
после S, выбираем P в 2/3 случаев.
"""
recent_play = p2hist[-1:]
digraphs = zip(p2hist, p2hist[1:])
followers = [b for a, b in digraphs if a == recent_play]
prediction = select_proportional(followers, options)
return ideal_response[prediction]
def digraph_event_greedy(p1hist, p2hist):
""" Если в прошлом раунде оппонент выбрал S,
но играет R в 2/3 случаев
после S, всегда выбираем P.
"""
recent_play = p2hist[-1:]
digraphs = zip(p2hist, p2hist[1:])
followers = [b for a, b in digraphs if a == recent_play]
prediction = select_maximum(followers, options)
return ideal_response[prediction]
strategies = [random_reply, single_event_proportional, single_event_greedy,
digraph_event_proportional, digraph_event_greedy]
def play_and_learn(opposition, strategies=strategies,
trials=1000, verbose=False):
strategy_range = range(len(strategies))
weights = [1] * len(strategies)
p1hist = []
p2hist = []
cum_score = 0
for trial in range(trials):
# выбираем свой вариант
our_moves = [strategy(p1hist, p2hist) for strategy in strategies]
i = choices(strategy_range, weights)[0]
our_move = our_moves[i]
# получаем вариант оппонента
opponent_move = opposition(p2hist, p1hist)
# определяем победителя
score = scorer[our_move + opponent_move]
if verbose:
print(f'{our_move} ~ {opponent_move} = {score:+d}'
f'\t\t{strategies[i].__name__}')
cum_score += score
# обновляем историю раундов и удельные веса стратегий
p1hist.append(our_move)
p2hist.append(opponent_move)
for i, our_move in enumerate(our_moves):
if scorer[our_move + opponent_move] == 1:
weights[i] += 1
print(f'---- vs. {opposition.__name__} ----')
print('Total score:', cum_score)
pprint(sorted([(weight, strategy.__name__) for weight, strategy in zip(weights, strategies)]))
if __name__ == '__main__':
def human(p1hist, p2hist):
return input(f'Choose one of {options!r}: ')
def fixed_ratio(p1hist, p2hist):
return choices(options, (1, 2, 3))[0]
def cycling(series):
iterator = cycle(series)
def cycle_opponent(p1hist, p2hist):
return next(iterator)
return cycle_opponent
play_and_learn(opposition=fixed_ratio)
play_and_learn(opposition=random_reply)
play_and_learn(opposition=cycling('RPRSS'))
play_and_learn(opposition=human, trials=10, verbose=True)Итак, бумага бьет камень. Это будет 1, и у нас появился идеальный ответ, т.е. победа. Что нам нужно делать. Мы выбираем среди своих стратегий, можно это делать случайным образом или пропорционально. Например, если камень будет в 2/3 случаев, то мы можем создавать диаграфы каждый раз, когда оппонент выбирает ножницы. Ведь мы знаем, что далее он выберет камень.
Вот такая серия стратегий. Неважно, какими они будут. Вам просто нужен набор стратегий. Я подготовил список, и алгоритм выбирает наш вариант. Как мы выбираем вариант. Мы берем свои стратегии и выбираем одну из них случайным образом в зависимости от удельного веса. Поначалу все веса одинаковые, т.е. все стратегии одинаково хороши.
Потом мы узнаем ход оппонента. Когда сын решит, что не будет есть брокколи, то я ему говорю, что наградой был бы десерт. Теперь нам нужно обновить историю раундов и удельные веса стратегий. Допустим, я больше не хочу так же часто использовать хитрость с десертом, но окончательно удалять ее из списка тоже не хочу.
Вот так выглядит алгоритм обучения методом проб и ошибок. Звучит впечатляюще? Ничего подобного. То, что можно написать в несколько строк, никогда не выглядит впечатляюще. С другой стороны, было бы неправильно говорить, что это не круто.
Вот этот неодушевленный предмет может обучаться и побеждать вас в "камень-ножницы-бумага" снова и снова. Интересно, сможете ли вы добиться результатов выше среднего. Вы увидите, что игра не особо веселая. Она быстро станет скучной, потому что компьютер учится по-настоящему быстро. Но вы сможете провести сто раундов примерно за пять минут. Под конец вы поймете, что случайного в ваших действиях немного. Пока никто не победил эту программу, потому что она изучит ваши "случайные" паттерны и полностью вас просчитает. О, погодите, Google и Facebook ведь уже делают это с вами.
На самом деле, конечно, наша работа во многом и заключается в том, что мы пытаемся вычислить намерения других людей. Это называется многорукий разветвленный подход (multi-armed branded approach). Его масштаб можно увеличить, чтобы охватить другие более интересные игры, которые есть у каждого.
Данный уровень предшествует задачам SMT Solvers (задачи выполнимости формул в теориях). Если вы хотите работать на очень техническом уровне и стать звездой на вечеринках в Кремниевой долине, то нужно знать данный термин. Вот как? Куплю вам выпить. Да, этот термин означает "satisfiability modulo theories" (задачи выполнимости формул в теориях).
3.3 SMT Solvers (задачи выполнимости формул в теориях)
Мы поднимаемся на уровень выше после алгоритмов поиска по дереву вариантов и SAT Solvers. Теперь у нас более сложная ситуация, чем обычная таблица истинности. Мы осуществляем поиск по графу, а не по дереву. Будем добавлять темпоральную логику (temporal logic).
Кто из вас слышал про темпоральную логику? Скорее всего, это будут те же люди, которые знали про TLA. Непонятно, почему я вижу меньше рук, ведь TLA, по сути, это и есть темпоральная логика. Под ней я понимаю то, что я не оцениваю статус по своей цели, т.е. добрался я до нее или нет. Это последовательность состояний, идущая подряд серия, например, цыпленок, а затем, может, яйцо. В какой последовательности они будут?
Вот у нас есть цели, в которых говорится об истинности (True) чего-либо. Что-то в конечном итоге всегда должно быть истинно. Приводятся умозаключения о последовательности состояний. Хорошим примером будет проблема философов за обедом.
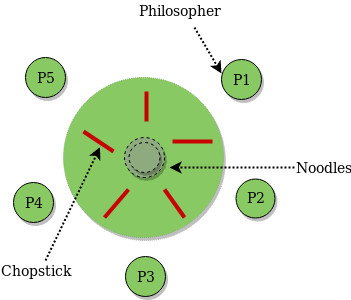
Кто из вас ее знает? Она великолепна. Моя картинка не появилась на экране, но на ней есть крылышки Buffalo Spurs и пять палочек для еды. На самом деле, нужны палочки в стиле династии Цинь, но у них всего пять штук. Чтобы удалось поесть, нужно две палочки.
Интересный момент в том, как мы будем это моделировать. Простой вариант — неограниченная модель, т.е. все палочки не использовались и находятся в руке философа слева или справа. Можно получить полное описание состояния с помощью пяти букв.
Состояние одной палочки ∈ { Не использовалась (U), ЛевыйФилософ (L), ПравыйФилософ (R) }
Состояние всех палочек ∈ {'UUUUU', 'UUUUL', 'UUURL', 'RUURL', ... }
Количество возможных состояний: 3⁵ = 243
Подразумеваемые состояния философов:
0 палочек в руках → Думает
1 палочка в руках → Пытается есть
2 палочки в руках → Ест
Неограниченные смены состояний палочек:
Не использовалась → ЛевыйФилософ
Не использовалась → ПравыйФилософ
ЛевыйФилософ → Не использовалась
ПравыйФилософ → Не использоваласьНа первый взгляд, количество состояний небольшое. Но они нам не интересны. Нам нужны все возможные пути по дереву состояний. Если вы знаете состояние, то у вас будет подразумеваемое состояние философов (думает, пытается есть, ест).
Если палочка не используется, то ее может взять левый или правый философ. Если на данный момент она используется, то может перейти в состояние не используемой. Получается, что в каждом состоянии есть только четыре варианта изменения. Похоже на модель Судоку.
Теперь у нас есть ключи к решению. Это наши стратегии. По поводу задачи обедающих философов интересно то, что большинство первым делом пытается решать методом, который звучит правильно, но по сути неправильный. Она очень познавательная, потому что учит тому, как сложно сделать корректную многопоточность.
Итак, очевидная стратегия заключается в том, что, испытывая голод, вы берете палочку слева. Когда освободится правая, вы тоже ее возьмете. Когда вы закончите с едой, по положите их обратно. Это будет стратегия D, которая всегда завершается взаимной блокировкой.
Стратегия D:
0 палочек в руке → ВзятьСлева
1 палочка в руке → ВзятьСправа
2 палочки в руке → ПоложитьОбе
Стратегия S:
Философ ноль всегда держит левую палочку
Стратегия H:
0 палочек в руке ∧ запроса нет → Поставить на очередь запрос на поесть
0 палочек в руке ∧ запрошено, доступных нет → Ждать
0 палочек в руке ∧ запрошено, доступные есть → Взять слева
1 палочка в руке → ВзятьСправа
2 палочки в руке → ПоложитьОбеСтратегия S по-настоящему ужасна. По ней первый философ берет палочку слева и никогда ее не кладет. Поэтому человек слева от него будет голодать. Здесь S означает Star, человека, который никогда не поест. Такой итог нежелателен.
Дальше стратегия H, happy. Можно создавать запросы на палочки. Стратегия не самая лучшая, но она работает. То есть, когда я хочу поесть, то выставляю запрос на поесть. Мы ведем очередь, кто будет есть следующим. Если вы не следующий на очереди, то ждете. Когда ваш запрос открывается, то вы получаете палочку слева, затем справа. Закончив с едой, вы кладете обе. Данная стратегия работает. Интересно отметить то, что не очевидно, какая из них работает, а какая проваливается.
Нам нужен инструмент, в который мы будем вводить свою стратегию. Если у него все будет получаться, то он сам сообщит об этом. При неудаче мы должны увидеть не сработавшую часть. Звучит как нечто полезное? А если в целом, вы когда-нибудь писали комплексный многопоточный код? Кто из вас? Так, а кто писал корректно работавший комплексный многопоточный код? Так, а у кого бывали пользователи, которые обходили блок (lock) и нарушали работу кода? В общем, кто писал код, который он сам считал бы корректным, да еще и с комплексом тестов, который доказал бы, что код всегда корректен? Да. Ну, вот тогда вам бы пригодились такого рода инструменты, потому что они могут это проверить для вас.
Еще вы могли бы генерировать все тесты, которые отражали бы все допустимые переходы состояний. Еще можно сделать так, чтобы программа сообщала об отклонении от модели.
По поводу данных программ для решения головоломок интересно то, что у них есть диаграммы переходов. В них используются темпоральные операторы (temporal operators), которые обозначают, что в конечном итоге предикат P будет истинным (True), либо что проблему создает именно человек, у которого палочка слева, и что ему нужно взять палочку справа.
Итак, пример программы для решения головоломок вроде предыдущих. Мы смотрим на одно из состояний и говорим, будет ли это желанным итогом, по поводу которого мы уже не будем беспокоиться. Темпоральная логика должна выразить этот момент, т.е. пришли ли мы к желательному состоянию.
Темпоральные операторы проверяют отношения между элементами последовательности состояний:
1. Предикат P будет истинным всегда: палочка находится в руках у 0 или 1 философа.
2. Предикат P будет в итоге истинным: философ с левой палочкой в руках в итоге получит правую.
3. Предикат P всегда будет в итоге истинным: закончив обед, философ всегда может поесть снова.
Например:
UUUUU -> ... -> UURLU -> ULUUU -> ... -> UURLU -> ...
^ ^
| |
Ф3 ест Ф3 думает Ф3 естЕсли вам хочется совсем уж углубиться в математику, то можно описать все это по модели TLA+. Это уже очень конкретная математика. По сути, генерируется график отслеживания всех путей и проверки всех темпоральных инвариантов. Я дам вам ссылку на хороший текст по этой теме.
Еще один хороший способ ослабить данную проблему придумали в Microsoft с помощью Z3. В Python есть пакет Z3Py, позволяющий пользоваться им.
Вот, мы узнали кое-что новое. Так что, если кто-нибудь когда-нибудь захочет еще раз написать комплексный многопоточный код, то не нужно делать это без его проверки на модели и генерации тестовых комплексов, чтобы быть уверенным в неизменной корректности кода.
Получается, что вы узнали кое-что новое и полезное. Хорошо!
4. AlphaZero
Следующая проблема немного сложнее:
- Научиться играть в самые сложные игры, известные человечеству, имея только правила игры;
- Выиграть у лучших игроков среди людей, а также у лучших подручных программ;
- Учитывать ограничение по времени: меньше дня.
Учить человека игре, только рассказав правила — жестоко. Допустим, я буду учить сына, только показывая ему возможные ходы в шахматах. Лучше применить обучение методом проб и ошибок. Я просто обыгрываю его раз за разом, а мой умный сын наблюдает за моими действиями и учится на своих поражениях. В конечном итоге он победит отца.
Я знаю, что так оно и работает, потому что именно так я учился играть в шахматы. Когда я был во втором классе, отец показал мне правила шахмат и начал меня обыгрывать много-много раз. Я никогда не сдавался. Когда я был в восьмом классе, с моим отцом случилось кое-что для него невиданное: он проиграл.
Потом данное событие утратило уникальность, а затем и редкость. Я стал лучше отца, но времени ушло много: со второго по восьмой класс. Нам нужно сжать шесть лет в шесть часов.
Так мы пришли к AlphaZero. Было весело, когда мы доказали, что она универсальна. То есть, мы дали ей правила шахмат, затем сёги (более сложная игра с вычислительной точки зрения), затем Го, затем добавили фигуру Lance (воин с копьем), которая двигается как конь, но на одно поле дальше, затем добавили фигуры, которые меняют сторону в случе выбытия и могут появляться в любой точке поля.
Мы ввели в программу только правила игры. В каждом случае, через 6-8 часов обучения AlphaZero научился побеждать у лучших в мире игроков среди людей, а еще — у лучших компьютерных программ.
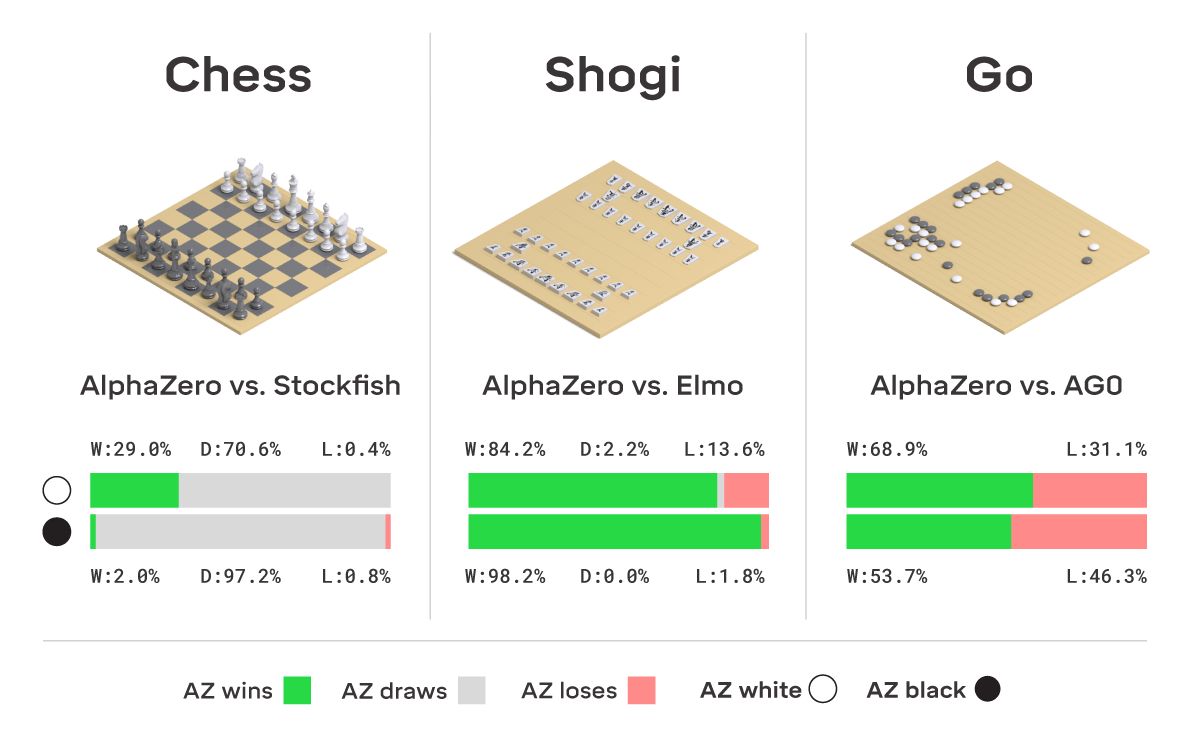
Причем те программы были специализированными, а AlphaZero — нет. Она знала только правила. Это означает, что мы можем решать широкий ассортимент проблем, просто описывая их содержание.
Нельзя забывать, что там использовались огромные вычислительные мощности. Но, все же, шесть часов — это впечатляет. Особенно, если знать, какие объемы вычислительной мощности были брошены на это. Это просто красота.
Вот типичный результат. Через несколько часов AlphaZero обыгрывает лучшую программу мира Stockfish:
Игра 3 - Белые: AlphaZero Черные: Stockfish
1. d4 Nf6 2. c4 e6 3. Nf3 b6 4. g3 Bb7 5. Bg2 Bb4+ 6. Bd2 Be7 7. Nc3 O-O
8. Qc2 Na6 9. a3 c5 10. d5 exd5 11. Ng5 Nc7 12. h4 h6 13. Nxd5 Ncxd5
14. cxd5 d6 15. a4 Qd7 16. Bc3 Rfe8 17. O-O-O Bd8 18. e4 Ng4
19. Bh3 hxg5 20. f3 f5 21. fxg4 fxg4 22. Bf1 gxh4 23. Bb5 Qf7
24. gxh4 Bf6 25. Rhf1 Rf8 26. Bxf6 gxf6 27. Rf4 Qg7 28. Be2 Qh6
29. Rdf1 g3 30. Qd3 Kh8 31. Qxg3 Rae8 32. Bd3 Bc8 33. Kb1 Rf7
34. Qf2 Bd7 35. h5 Ref8 36. Bc2 Be8 37. Rf3 Re7 38. Rxf6 Qxf6
39. Qxf6+ Rxf6 40. Rxf6 Kg7 41. Rxd6 Bxh5 42. Kc1 Re5 43. a5 bxa5
44. Kd2 Be8 45. Ra6 Rh5 46. Bd3 a4 47. d6 Bf7 48. d7 Rh8 49. e5 1-0Данную партию очень интересно отыграть, если вам интересны шахматы. Просто двигаем фигуры и следим за красотой. Возможно, это лучшая партия в шахматы, сыгранная за всю историю.
Вся эта красота поднимает вопрос о том, что мы обо всем этом думаем. Две оценки приводятся в статье про AlphaGo, ссылку на нее я вам уже дал. Статья платная и доступна через журнал Science. Но у авторов есть бесплатный препринт.
По их мнению, результаты показывают, что программа общего назначения, которая обучается по методу проб и ошибок, в состоянии обучаться с чистого листа, то есть вообще без ввода специализированной информации или накопленных человеком знаний. Программа может достичь успеха во многих областях, т.е. сверхчеловеческой эффективности во многих трудных играх через несколько часов. Просто зверски.
Гарри Каспаров дал комментарий, выглядящий несколько эгоистично: "Не могу скрыть своего удовлетворения тем, что она играет в очень динамичном стиле, очень похожем на мой!" Звучит эгоистично, если не учитывать того, что Каспаров играл очень круто. И ведь данная вещь научилась играть как человек. Она могла ставить людям ловушки.
Так, хорошо. Мне дали стоп-сигнал. Это означает, что мне нужно закрыться через пять минут. Это очень хорошо. На самом деле, я иду по графику. Потрясающе.
Итак, код, который можно было бы запустить. AlphaZero — открытый продукт, но ее достижения мы добавили в программу Leela Chess Zero. Она тоже общедоступная и сделана на основе Meson и Python 3, но запускает, в основном, код CUDA на графическом процессоре.
Я бы сказал, что там все сделано на Python 3, но просто Python недостаточно быстрый. C тоже недостаточно быстрый. Что делает программа: она генерирует код, который можно запустить на вашем графическом процессоре, и это прекрасно. Так что можно скачать по ссылке и начать игру в шахматы с лучшими программами мира, используя именно эти методики.
Вот поиск по дереву методом Монте-Карло (Monte Carlo tree search). По сути, в нем выбирается (Selection) паттерн для запуска. Прогоним его до самого завершения игры по разным маршрутам (Expansion) и определим путь к победе и поражению. Будет много симуляций (Simulation). В конце происходит обратное распространение результатов (Backpropagation) с попутным взвешиванием. В итоге делается вывод об удачности конкретного хода.
По сути, это почти наш алгоритм обучения методом проб и ошибок, о котором я говорил раньше. Просто в нем используется дерево.
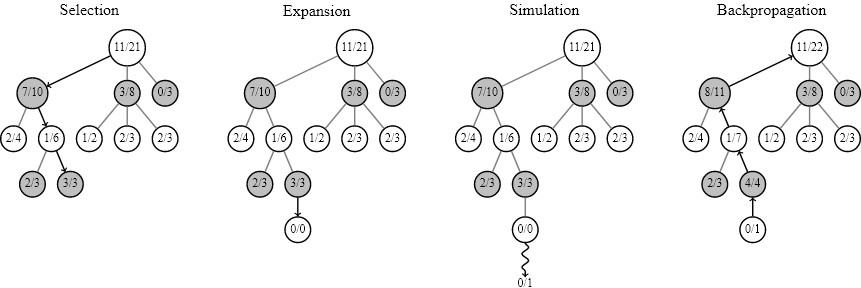
Если вам нужно полное описание алгоритма, то в общих чертах оно приводится в статье по DeepMind:
AlphaZero заменяет собой ручное накопление знаний и пошаговое развитие специализированных направлений, которое затем используется в традиционных игровых программах, на глубокие нейронные сети, генеральные алгоритмы обучения на основе принципа проб и ошибок, а также генеральный алгоритм поиска по дереву.
Вместо созданной вручную функции оценки и эвристики упорядочения перемещений AlphaZero использует глубокую нейронную сеть (p, v) = fθ (s) с параметрами θ. Данная нейронная сеть fθ (s) принимает положение на игровом поле s в качестве входных данных и выводит вектор вероятностей ходов p с компонентами pa = Pr (a|s) для каждого действия a и скалярное значение v, оценивающее ожидаемый результат z для игры из позиции s, v ≈ E [z | s]. AlphaZero изучает данные вероятности ходов и оценки значений исключительно на собственном опыте; затем они используются в качестве направляющих поиска в будущих играх.
Вместо альфа-бета отсечения со специализированными для конкретных областей расширениями AlphaZero использует универсальный алгоритм поиска по дереву методом Монте-Карло (MCTS). Каждый поиск состоит из серии симуляций игр с самим собой, которые проходят по дереву от корневого состояния sroot до конечного состояния leaf. Каждая симуляция выполняется путем выбора в каждом состоянии s хода a с низким числом посещений (которые ранее изучались нечасто), высокой вероятностью совершения и высоким значением (усредненным по конечным состояниям симуляций, в которых совершен выбор a из s) в соответствии с используемой нейронной сетью fθ. Поиск возвращает вектор π, представляющий собой распределение вероятностей по ходам, πa = Pr (a | sroot).
Параметры θ глубокой нейронной сети в AlphaZero обучаются методом проб и ошибок в играх с самим собой, начиная с рандомно инициализированных параметров θ. В каждой игре выполняется поиск MCTS из текущей позиции sroot = st на ходу t, а затем производится выбор хода при ~ πt пропорционально (для исследования) либо жадно (для использования) относительно количества посещений при корневом состоянии. В конце игры конечная позиция sT оценивается в соответствии с правилами игры в целях вычисления результата игры z: -1 при поражении, 0 при ничьей и +1 при победе. Параметры θ нейронной сети обновляются, чтобы минимизировать ошибку между предсказанным результатом vt и результатом игры z, а также максимизировать сходство между вектором стратегий pt и вероятностями поиска πt. Обновленные параметры используются в последующих играх с самим собой.
5. Заключение
Поговорим о будущем. Если вам хочется услышать полноценное выступление про будущее, куда это все движется, то лучше уйти. Здесь риск в том, что будущее не известно, и его трудно предсказывать. Нам нужно спрашивать себя, закончится ли все плохо. Кто думает, что все закончится плохо? Вообще, основание думать именно так, оно есть. Это правда.
Вообще есть большой мыслитель, который глубоко задумывался об этой проблеме. Который действительно сражался с этими всеми машинами.

Сначала он побеждал машины, а потом проиграл одной. В дальнейшем он проигрывал уже чаще. Один из самых умных людей в мире много размышлял об этом всем. Мне очень нравится его книга. Гарри Каспаров не думает, что все закончится плохо.
Я очень рекомендую его книгу Deep Thinking. Читается как художественная литература, страницы перелистываешь одну за другой. В этой книге много говорится про искусственный интеллект. Не забывайте, он был одним из умнейших и противостоял компьютеру, когда все это только начиналось. В конечном итоге он проиграл.
В этой книге есть очень глубокие мысли о том, каким будет наше взаимодействие с машинами в будущем. О том, какие профессии они вытеснят. В чем они будут нам помогать, в чем будут вредить. Как они будут адаптироваться.
Мне кажется, мы живем в замечательное время. Спасибо, что пришли.